¿HACIA DÓNDE SE MOVERÁ?

Para saber la dirección del movimiento de un objeto sobre el que se aplican varias fuerzas a la vez, hay que conocer primero las características de cada fuerza por separado. Conviene considerar al conjunto de interacciones como un sistema de fuerzas.

Si dos fuerzas iguales en magnitud y dirección se aplican a un cuerpo en sentidos opuestos, éste no se moverá porque los efectos se contrarrrestan.
Un ejemplo de esto se tiene  cuando dos personas jalan con la misma fuerza los dos extremos de una cuerda en sentido contrario.

El análisis de las fuerzas que intervienen en un sistema es indispensable, por ejemplo, para los ingenieros que construyen puentes, edificios o plataformas petroleras, porque de sus predicciones y cálculos depende que las edificaciones  se muevan controladamente o permanezcan estáticas.

Cuando dos o mas fuerazas se aplican en la misma dirección, sin importar que tengan sentidos contrarios, se denominan fuerzas colineales. En este caso, si tienen el mismo sentido, sus magnitudes se suman; si tienen sentido contrario, las magnitudes se restan, en forma similar a como se procede con la recta numérica.

Cuando las fuerzas aplicadas no son colineales, la fuerza resultante ya no es simplene una suma aritmética. El procedimiento gráfico para sumar fuerzas en este caso es el método del poligono que es el siguiente:

1. Cada fuerza se representa como una flecha. Puesto que las fuerzas se ejercen sobre el mismo punto de aplicación, éstas se trazan a partir de este punto , conservando las caracteristicas de magnitud, sentido y dirección de las fuerzas que se quiere representar.
2. Después, se reacomodan las flechas de manera que se coloca la punta de una flecha con el extremo de otra, respetando la longitud, la dirección y el sentdio originales.
3. La resultante se obtiene trazando una línea desde el origen de la primera flecha, hasta la punta la última flecha, es decir, del punto de aplicación al punto final de las fuerzas trazadas

ANALIZEN EL PROBLEMA QUE SE PLANTEO EN LA GUIA:

Van a necesitar hojas y transportador
Analicen la situación que se presenta:
Dos pescadores jalan una red llena de peces, aplicando fuerzas de la misma magnitud, pero ocn diferente dirección. Una de las personas jala la red con una fuerza de 5 unidades en una dirección de 45° hacia la lancha. Esta fuerza F2 ¿Hacia donde se movera la red si la fuerza aplicada es de 5 unidades?

En otra hoja utiliza el método del poligono para obtener la resultante de las fuerzas aplicadas por los pescadores sobre la red.
Indiquen la magnitud, dirección y sentido de la fuerza resultante que mueve la red.

ANALIZA:

¿El sentido del movimiento de la red es el mismo que  el de las fuerzas aplicadas por los pescadores? Expliquen.

b) Proporcionen un ejemplo en el que  una fuerza suple la acción de dos fuerzas concurrentes simultáneas.

DINAMOMETRO

MAQUINAS COMPUESTAS O COMPLEJAS

MAQUINAS COMPUESTAS O COMPLEJAS

REALIZA UN RESUMEN E INVESTIGA COMO SERIAN LAS PARTES DE UNA MÁQUINA DE COSER, COMO UNA MAQUINA COMPUESTA. 

Las maquinas compuestas son una union de varias maquinas simples, de forma q la salida de cada una de ellas esta directamente conectada a la entrada de la siguiente hasta consegui el efecto deseado.

Ya se sabe q las maquinas simples reducen o multiplican el trabajo, una caracteristica de la maquinas compuestas es q tienen moviemiento.

Las máquinas simples, por su parte, se agrupan dando lugar a los mecanismos, cada uno encargado de hacer un trabajo determinado. Si analizamos un taladro de sobremesa podremos ver que es una máquina compuesta formada por varios mecanismos: uno se encarga de crear un movimiento giratorio, otro de llevar ese movimiento del eje del motor al del taladro, otro de mover el eje del taladro en dirección longitudinal, otro de sujetar la broca, son formadas por diferentes piezas: ejes, palancas, muelles.etc…

Cada una de las piezas q conforman una maquina compuesta se llama OPERADOR, hay dos tipos de operadores MECANICOS y ENERGETICOS.
Mecánicas: las más importantes son:
Ruedas: que permiten desplazarse
Los ejes: sirven de punto de apoyo para las ruedas
Engranajes: son rueditas detalladas que sirven para mover las ruedas

Energéticas: las más importantes son:
Los muelles, baterías o pilas: acumulan energía en movimiento
Los motores: transforman la energía en movimiento

MÁQUINA SIMPLE

IDENTIFCA :
¿QUE ES UNA MÁQUINA SIMPLE?

¿CUALES SON SUS PARTES?
¿QUE ES UNA POLEA Y QUE ES UN PLANO INCLINADO? IDENTIFICA SUS PARES
MENCIONA TRES EJEMPLOS

Máquinas simples

Se denominan máquinas a ciertos aparatos o dispositivos que se utilizan para transformar o compensar una fuerza resistente o levantar un peso en condiciones más favorables.

Palanca para sacar un clavo

Es decir, realizar un mismo trabajo con una fuerza aplicada menor, obteniéndose una ventaja mecánica.

Esta ventaja mecánica comporta tener que aplicar la fuerza a lo largo de un recorrido (lineal o angular) mayor. Además, hay que aumentar la velocidad para mantener la misma potencia.

Las primeras máquinas eran sencillos sistemas que facilitaron a hombres y mujeres sus labores, hoy son conocidas como máquinas simples.

La rueda, la palanca, la polea simple, el tornillo, el plano inclinado, el polipasto, el torno y la cuña son algunas máquinas simples. La palanca y el plano inclinado son las más simples de todas ellas.

En general, las maquinas simples son usadas para multiplicar la fuerza o cambiar su dirección, para que el trabajo resulte más sencillo, conveniente y seguro.

Ejemplos de máquinas simples

Palanca

Una palanca es, en general, una barra rígida que puede girar alrededor de un punto fijo llamado punto de apoyo o fulcro.

Conocida máquina simple: la palanca

La fuerza que se aplica se suele denominar fuerza motriz o potencia y la fuerza que se vence se denomina fuerza resistente, carga o simplemente resistencia.

Polea

La polea sirve para elevar pesos a una cierta altura. Consiste en una rueda por la que pasa una cuerda a la que en uno de sus extremos se fija una carga, que se eleva aplicando una fuerza al otro extremo. Su función es doble, puede disminuir una fuerza, aplicando una menor, o simplemente cambiar la dirección de la fuerza. Si consta de más de una rueda, la polea amplifica la fuerza. Se usa, por ejemplo, para subir objetos a los edificios o sacar agua de los pozos.

Polea simple

Las poleas pueden presentarse de varias maneras:

Polea fija: solo cambia la dirección de la fuerza. La polea está fija a una superficie.

Polea móvil: se mueve junto con el peso, disminuye el esfuerzo al 50%.

Polea pasto, polipasto o aparejo: Formado por tres o más poleas en línea o en paralelo, se logra una disminución del esfuerzo igual al número de poleas que se usan.

Polipasto

Se llama polipasto a un mecanismo que se utiliza para levantar o mover una carga aplicando un esfuerzo mucho menor que el peso que hay que levantar.

Estos mecanismos se utilizan mucho en los talleres o industrias que manipulan piezas muy voluminosas y pesadas porque facilitan la manipulación, elevación y colocación de estas piezas pesadas, así como cargarlas y descargarlas de los camiones que las transportan.

Esquema funcional de un polipasto

Suelen estar sujetos a un brazo giratorio que hay acoplado a una máquina, o pueden ser móviles guiados por raíles colocados en los techos de las naves industriales.

Los polipastos tienen varios tamaños o potencia de elevación, los pequeños se manipulan a mano y los más grandes llevan incorporados un motor eléctrico.

Rueda

Máquina simple más importante que se conoce, no se sabe quién y cuándo la descubrió o inventó; sin embargo, desde que el hombre utilizó la rueda la tecnología avanzó rápidamente, podemos decir que a nuestro alrededor siempre está presente algún objeto a situación relacionado con la rueda, la rueda es circular. 

Plano inclinado

El plano inclinado permite levantar una carga mediante una rampa o pendiente. Esta máquina simple descompone la fuerza del peso en dos componentes: la normal (que soporta el plano inclinado) y la paralela al plano (que compensa la fuerza aplicada). De esta manera, el esfuerzo necesario para levantar la carga es menor y, dependiendo de la inclinación de la rampa, la ventaja mecánica es muy considerable.

Al igual que las demás máquinas simples cambian fuerza por distancias. El plano inclinado se descubre por accidente ya que se encuentra en forma natural, el plano inclinado es básicamente un triángulo donde su utiliza la hipotenusa, la función principal del plano inclinado es levantar objetos por encima de la Horizontal.

Plano inclinado

El plano inclinado puede presentarse o expresar también como cuña o tornillo. 

Cuña

Se forma por dos planos inclinados opuestos, las conocemos comúnmente como punta, su función principal es introducirse en una superficie.

Ejemplo: Flecha, hacha, navaja, desarmado, picahielo, cuchillo.

Tornillo

Plano inclinado enrollado, su función es la misma del plano inclinado pero utilizando un menor espacio.

Ejemplos: escalera de caracol, carretera, saca corcho, resorte, tornillo, tuerca, rosca.

Nivel o torno

Máquina simple constituida por un cilindro en donde enredar una cuerda o cadena, se hace girar por medio de una barra rígida doblada en dos ángulos rectos opuestos. Como todas las máquinas simples el torno cambia fuerza por distancia, se hará un menor esfuerzo entre más grande sea el diámetro.

Ejemplos: grúa, fonógrafo, pedal de bicicleta, perilla, arranque de un auto antiguo, grúa, ancla, taladro manual.

PALANCAS

REALIZA UN CUADRO SINOPTICO DE ESTE TEMA


El hombre, desde los inicios de los tiempos ha ideado mecanismos que le permitan ahorrar energía y con ello lograr que sus esfuerzos físicos sea cada vez menores.
Entre los diversos mecanismos para hacer más eficientes sus esfuerzos se pueden citar las poleas, los engranajes y las palancas.
La palanca es una máquina simple que se emplea en una gran variedad de aplicaciones.
Probablemente, incluso, las palancas sean uno de los primeros mecanismos ingeniados para multiplicar fuerzas. Es cosa de imaginarse el colocar una gran roca como puerta a una caverna o al revés, sacar grandes rocas para habilitar una caverna.
Con una buena palanca es posible mover los más grandes pesos y también aquellos que por ser tan pequeños también representan dificultad para tratarlos.

Galileo habría "movido" la Tierra

Se cuenta que el propio Galileo Galilei habría dicho: "Dadme un punto de apoyo y moveré el mundo". En realidad, obtenido ese punto de apoyo y usando una palanca suficientemente larga, eso es posible.
En nuestro diario vivir son muchas las veces que “estamos haciendo palanca”. Desde mover un dedo o un brazo o un pie hasta tomar la cuchara para beber la sopa involucra el hacer palanca de una u otra forma.
Ni hablar de cosas más evidentes como jugar al balancín, hacer funcionar una balanza, usar un cortaúñas, una tijera, un diablito (sacaclavos), etc.
Casi siempre que se pregunta respecto a la utilidad de una palanca, la respuesta va por el lado de que “sirve para multiplicar una fuerza”, y eso es cierto pero prevalece el sentido que multiplicar es aumentar, y no es así siempre, a veces el multiplicar es disminuir (piénsese en multiplicar por un número decimal, por ejemplo).
¿Qué es una palanca?
Básicamente está constituida por una barra rígida, un punto de apoyo (se le puede llamar “fulcro”) y dos fuerzas (mínimo) presentes: una fuerza (o resistencia) a la que hay que vencer (normalmente es un peso a sostener o a levantar o a mover en general) y la fuerza (o potencia) que se aplica para realizar la acción que se menciona. La distancia que hay entre el punto de apoyo y el lugar donde está aplicada cada fuerza, en la barra rígida, se denomina brazo. Así, a cada fuerza le corresponde un cierto brazo.
Como en casi todos los casos de máquinas simples, con la palanca se trata de vencer una resistencia, situada en un extremo de la barra, aplicando una fuerza de valor más pequeño que se denomina potencia, en el otro extremo de la barra.
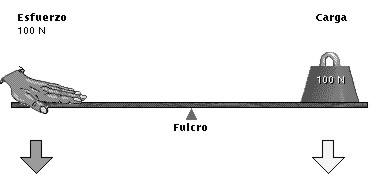
En una palanca podemos distinguir entonces los siguientes elementos:
El punto de apoyo o fulcro.
Potencia: la fuerza (en la figura de abajo: esfuerzo) que se ha de aplicar.
Resistencia: el peso (en la figura de abajo: carga) que se ha de mover.

Brazo de potencia	Brazo de resistencia

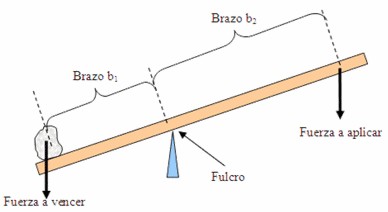
El brazo de potencia (b₂) : es la distancia entre el fulcro y el punto de la barra donde se aplica la potencia.
El brazo de resistencia (b₁): es la distancia entre el fulcro y el punto de la barra donde se encuentra la resistencia o carga.
¿Cuántos tipos de palanca hay?

La ubicación del fulcro respecto a la carga y a la potencia o esfuerzo, definen el tipo de palanca

Según lo visto en la figura y lo definido en el cuadro superior, hay tres tipos de palancas:
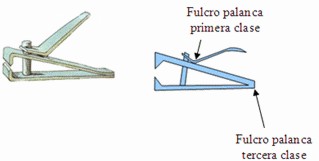
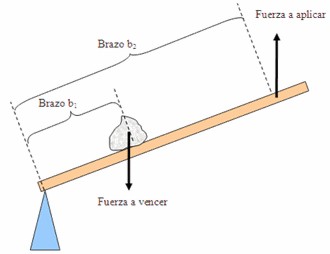
Palanca de primer tipo o primera clase o primer grupo o primer género:
Se caracteriza por tener el fulcro entre la fuerza a vencer y la fuerza a aplicar.

Palanca de primera clase

 
Esta palanca amplifica la fuerza que se aplica; es decir, consigue fuerzas más grandes a partir de otras más pequeñas.
Por ello, con este tipo de palancas pueden moverse grandes pesos, basta que el brazo b1 sea más pequeño que el brazo b2.
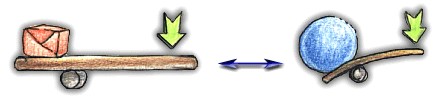
Algunos ejemplos de este tipo de palanca son: el alicates, la balanza, la tijera, las tenazas y el balancín.

Palancas de primera clase

Algo que desde ya debe destacarse es que al accionar una palanca se producirá un movimiento rotatorio respecto al fulcro, que en ese caso sería el eje de rotación.
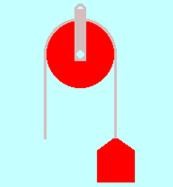
Palanca de segundo tipo o segunda clase o segundo grupo o segundo género:
Se caracteriza porque la fuerza a vencer se encuentra entre el fulcro y la fuerza a aplicar.

Palanca de segunda clase

Este tipo de palanca también es bastante común, se tiene en lo siguientes casos: carretilla, destapador de botellas, rompenueces.

Palancas de segunda clase

También se observa, como en el caso anterior, que el uso de esta palanca involucra un movimiento rotatorio respecto al fulcro que nuevamente pasa a llamarse eje de rotación.
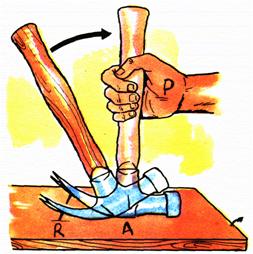
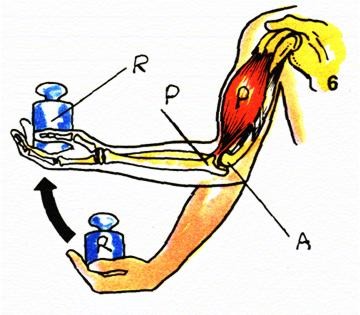
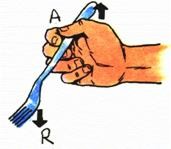
Palanca de tercer tipo o tercera clase o tercer grupo:
Se caracteriza por ejercerse la fuerza “a aplicar” entre el fulcro y la fuerza a vencer.

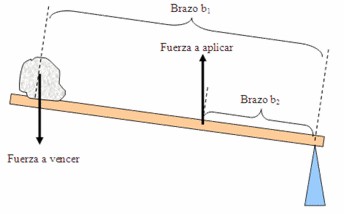Palanca de tercera clase

Este tipo de palanca parece difícil de encontrar como ejemplo concreto, sin embargo… el brazo humano es un buen ejemplo de este caso, y cualquier articulación es de este tipo, también otro ejemplo lo tenemos al levantar una cuchara con sopa o el tenedor con los tallarines, una corchetera funciona también aplicando una palanca de este tipo.

Palancas de tercera clase

Este tipo de palanca es ideal para situaciones de precisión, donde la fuerza aplicada suele ser mayor que la fuerza a vencer.
Y, nuevamente, su uso involucra un movimiento rotatorio.
Hemos visto los tres tipos de palancas, unos se usan más que otros, pero los empleamos muy a menudo, a veces sin siquiera darnos cuenta, y sin pensar en el tipo de palanca que son cuando queremos aplicar su funcionamiento en algo específico.
En algunas ocasiones, ciertos artefactos usan palancas de más de un tipo en su funcionamiento, son las palancas múltiples.
Palancas múltiples: Varias palancas combinadas.
Por ejemplo: el cortaúñas es una combinación de dos palancas, el mango es una combinación de 2º género que presiona las hojas de corte hasta unirlas. Las hojas de corte no son otra cosa que las bocas o extremos de una pinza y, constituyen, por tanto, una palanca de tercer género.

Otro tipo de palancas múltiples se tiene en el caso de una máquina retroexcavadora, que tiene movimientos giratorios (un tipo de palanca), de ascenso y descenso (otra palanca) y de avanzar o retroceder (otra palanca).
Ley de las palancas
Desde el punto de vista matemático hay una ley muy importante, que antiguamente era conocida como la “ley de oro”, nos referimos a la Ley de las Palancas:

El producto de la potencia por su brazo (F2 • b2) es igual al producto de la resistencia por el brazo suyo (F1 • b1)

lo cual se escribe así:

F1 • b1 = F2 • b2

lo que significa que:

Trabajo motor = Trabajo resistente

Llamando F1 a la fuerza a vencer y F2 a la fuerza a aplicar y recordando que b1 es la distancia entre el fulcro y la fuerza a vencer y b2 la distancia entre el fulcro y el lugar donde se ha de aplicar la fuerza F2. En este caso se está considerando que las fuerzas son perpendiculares a los brazos.
Y es válida para todo tipo de palancas. 
Ahora bien, ¿en qué se sostiene la Ley de las Palancas?
En un concepto mucho más amplio, el concepto de “torque”.
Al comentar las características de cada tipo de palanca, dijimos que su uso involucra siempre un movimiento rotatorio. Bien, cada vez que se realiza, o se intenta realizar, un movimiento rotatorio se realiza lo que se denomina “torque”.
Torque es la acción que se realiza mediante la aplicación de una fuerza a un objeto que debido a esa fuerza adquiere o puede adquirir un movimiento rotatorio.
Abrir una puerta involucra la realización de torque. El eje de rotación son las bisagras.
Abrir un cuaderno involucra la realización de torque. El eje de rotación es el lomo o el espiral.
Jugar al balancín es hacer torque. El eje de rotación es el punto de apoyo.
Al mover un brazo se realiza torque. El eje de rotación es el codo.
Dos situaciones excepcionales hay que distinguir:
- Cuando se aplica la fuerza en el eje de rotación no se produce rotación, en consecuencia no hay torque. ¿Se imaginan ejercer una fuerza en una bisagra para abrir una puerta?
- Cuando se aplica la fuerza en la misma dirección del brazo tampoco se realiza rotación, por lo tanto tampoco hay torque. O, mejor dicho, el torque es nulo. Imagínense atar una cuerda al borde de la tapa de un libro y tirar de él, paralelo al plano del libro, tratando de abrirlo.
Ya que mencionamos el caso de situaciones particulares donde el torque que se realiza resulta ser nulo, destaquemos también que el torque es máximo cuando el ángulo entre el brazo y la fuerza a aplicar es un ángulo recto (90º y 270º). Otros casos, donde el ángulo entre la fuerza aplicada y el brazo no es ni recto ni nulo ni extendido (0º o 180º) necesitan de matemática que en estos momentos no están al alcance.

¿Cómo se pueden representar las fuerazas?

Ciertas cantidades en la fisica, llamadas escalares, quedan exclusivamente determinadas con un número y una unidad de medida, como sucede con el tiempo. Así afirmamos que un suceso ocurrió en 2 horas. Otras cantidades en cambio, llmadas vectoriales, requieren además , una dirección y un sentido para que queden totalmente definidas. Hemos mencionado en secuencias previas al desplazamiento y la velocidad ques on, por supuesto, cantidades vectoriales. Es claro que n es lo mismo caminar 5 kilómetros hacia el norte que 5 kilómetros hacia el sur.

De la misma manera, no obtenemos el mismo resultado si lanzamos una pelota de básquetbol hacia la canasta del equipo contrincante que hacia la propia, aunque necesitemos la misma magnitud de fuerza para arrojarla. ¿ Qué tipo de cantidad será entonces la fuerza? Es, tambien, una cantidad vectorial C.

Como la fuerza es un vector, se puede representar mediante una flecha cuya longitud indique qué cantidad de fuerza se aplica y cuál es su dirección y sentido. Cuando se ejercen diversas fuerzas sobre un cuerpo, una representación de vectores permite analizzr qué efecto se producirá como resultado de aplicar todas las fuerzas simultáneamente.

El punto de aplicación de cada fuerza está representado por el punto inicial de la flecha; la dirección es el ángulo que forma la flecha con el eje horizontal, el sentido es hacia donde apuna la flecha y la magnitud de la fuerza, es proporcional al tamaño total de la flecha, medido desde el punto de aplicación  hasta la punta de la misma, trazada en una escala apropiada de longitud.

 

¿CUÁLES SON LAS VENTAJAS DE USAR FLECHAS PARA REPRESENTAR LAS FUERZAS?

ERASE UNA VEZ LOS INVENTROES "NEWTON"

REALIZA UN RESUMEN DE ESTOS VIDEOS.

FUERZAS Y COMO ACTUAN LAS FUERZAS

REALIZA RESUMEN DE CADA UNO DE LOS VIDEOS QUE YA SE VIERON EN CLASE

VIDEOS FRICICIÓN

Realiza un resumen del video